Ứng Dụng Công Thức Tìm Nguyên Hàm Của Hàm Số Căn Bậc Hai Của Tanx - BITEXEDU

Ở những nội dung bài viết trước, diễn đàn vẫn share về phong thái tính những tích phân của những hàm số vô tỉ $\int{\dfrac{1}{1+{{x}^{n}}}dx}$  với $n=1,n=2,n=3$ và $n=4$.
Tiếp theo đuổi loạt nội dung bài viết này, Cửa Hàng chúng tôi trình diễn phương pháp tính vẹn toàn hàm của hàm số $y=\sqrt{\tan x}$. Những bài xích tập dượt này tuy rằng không hỗ trợ ích được rất nhiều vô kì ganh đua Trung học tập phổ thông vương quốc. Tuy nhiên nó sẽ hỗ trợ chúng ta tập luyện nhiều về kĩ năng đo lường và tính toán và thay đổi. Một loại khá quan trọng mang đến những nhiều người đang mong muốn học tập những ngành tương quan cho tới kinh nghiệm.

Tìm vẹn toàn hàm của hàm số $y=\sqrt{\tan x}$

Trước khi cút vô đo lường và tính toán, tớ nói lại công thức sau:

Bạn đang xem: Ứng Dụng Công Thức Tìm Nguyên Hàm Của Hàm Số Căn Bậc Hai Của Tanx - BITEXEDU

$$\int{\dfrac{dx}{a{{x}^{2}}+bx+c}=\dfrac{2}{\sqrt{-\Delta }}\arctan \dfrac{2ax+b}{\sqrt{-\Delta }}+C}$$

Trong cơ $\Delta ={{b}^{2}}-4ac<0$.

Đặt $t=\sqrt{\tan x}\Rightarrow x=\arctan {{t}^{2}}\Rightarrow dx=\dfrac{2tdt}{1+{{t}^{4}}}$.

Khi cơ $\displaystyle I=\int{\sqrt{\tan x}dx\Rightarrow \int{\dfrac{2{{t}^{2}}dt}{1+{{t}^{4}}}}}$

Ta có: $\dfrac{2{{t}^{2}}}{1+{{t}^{4}}}=\dfrac{At+B}{{{t}^{2}}+\sqrt{2}t+1}+\dfrac{Ct+D}{{{t}^{2}}-\sqrt{2}t+1}$

Bằng cách thức thông số biến động, giải hệ tứ phương trình tuyến tính

$$\left\{ \begin{aligned}  & A+C=0 \\ & -A\sqrt{2}+B+C\sqrt{2}+D=2 \\ & A-B\sqrt{2}+C+D\sqrt{2}=0 \\ & B+D=0 \\\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}  & A=-\dfrac{\sqrt{2}}{2} \\ & B=0 \\ & C=\dfrac{\sqrt{2}}{2} \\ & D=0 \\\end{aligned} \right.$$

Kết quả

Lưu nhì nghiệm $x$ vô $A$ và $y$ vô $B$

Vậy $\dfrac{1}{1+{{t}^{4}}}=-\dfrac{\sqrt{2}}{4}\left[ \dfrac{2t+\sqrt{2}-\sqrt{2}}{{{t}^{2}}+\sqrt{2}t+1}-\dfrac{2t-\sqrt{2}+\sqrt{2}}{{{t}^{2}}-\sqrt{2}t+1} \right]$

Suy ra:

Xem thêm: 4 cách làm bánh với bột mì số 8 mềm xốp thơm ngon

$$\int{\dfrac{2{{t}^{2}}dt}{1+{{t}^{4}}}=\dfrac{\sqrt{2}}{4}\ln \left| \dfrac{{{t}^{2}}-\sqrt{2}t+1}{{{t}^{2}}+\sqrt{2}t+1} \right|}+\dfrac{\sqrt{2}}{2}\arctan \dfrac{2t+\sqrt{2}}{\sqrt{2}}+\dfrac{\sqrt{2}}{2}\arctan \dfrac{2t-\sqrt{2}}{\sqrt{2}}+C$$

Do đó

$$\int{\dfrac{2{{t}^{2}}dt}{1+{{t}^{4}}}=\dfrac{\sqrt{2}}{4}\ln \left| \dfrac{{{t}^{2}}-\sqrt{2}t+1}{{{t}^{2}}+\sqrt{2}t+1} \right|}+\dfrac{\sqrt{2}}{2}\arctan \left( \sqrt{2}t+1 \right)+\dfrac{\sqrt{2}}{2}\arctan \left( \sqrt{2}t-1 \right)+C$$

Kiểm tra bên trên PC Casio fx-580VNX

Mở w8 nhập hàm số

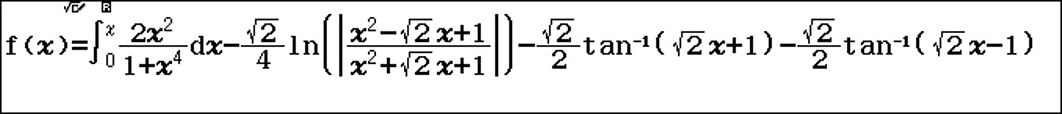
Cho $x$ chạy

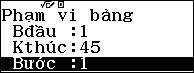
Kết ngược là

$45$ độ quý hiếm của $x$ đều mang đến thành quả là hằng $C\approx 0$.

Kết luận$$\int{\sqrt{\tan x}dx=\dfrac{\sqrt{2}}{4}\ln \left| \dfrac{{{t}^{2}}-\sqrt{2}t+1}{{{t}^{2}}+\sqrt{2}t+1} \right|}+\dfrac{\sqrt{2}}{2}\arctan \left( \sqrt{2}t+1 \right)+\dfrac{\sqrt{2}}{2}\arctan \left( \sqrt{2}t-1 \right)+C$$

trong cơ $t=\sqrt{\tan x}$.

Xem thêm: Chậu Cảnh Lục Giác KT: 45 - 60 - 70 - 80cm

Đây vẫn chính là phần đo lường và tính toán sau cùng vô nội dung bài viết. Tuy nhiên, nhằm mục tiêu mong muốn các  Tại nội dung bài viết sau, diễn đàn tiếp tục share cho tới quý khách một vài dụng cụ đo lường và tính toán bên trên PC nhằm mục tiêu gom những bạn cũng có thể thuận tiện rộng lớn khi đo lường và tính toán và đánh giá những luật lệ tính phức tạp. Trân trọng.

TS. Nguyễn Thái Sơn – Vũ Nhân Khánh