
Trong quãng thời hạn ngồi bên trên ghế mái ấm ngôi trường, những em học viên sẽ tiến hành nghe biết những hình nhiều giác, vô bại liệt hình tam giác là hình tuy nhiên những em sẽ tiến hành nghe biết trước tiên. Dù vậy, kỹ năng và kiến thức về hình tam giác lưu giữ tầm quan trọng vô nằm trong cần thiết vô toàn bộ những bài bác thi đua và bài bác đánh giá của những em. Bài viết lách bên dưới đó là tổng phù hợp dạng bài bác về tam giác, rất đầy đủ khái niệm, đặc thù và phương thức minh chứng của những toàn bộ những loại hình tam giác. Nào, những em hãy nằm trong HOCMAI vô bài bác nhé!
A. LÝ THUYẾT VỀ TAM GIÁC
I. Khái niệm tam giác
Tam giác là 1 trong những loại nhiều giác đơn và là nhiều giác sở hữu con số cạnh tối thiểu trong số loại nhiều giác (3 cạnh), tam giác sở hữu tía đỉnh là tía điểm ko trực tiếp sản phẩm nhau và tía cạnh là tía đoạn trực tiếp nối những đỉnh lại cùng nhau. Tổng của tía góc vô của một tam giác vì thế 180 chừng.
Bạn đang xem: Tổng hợp dạng bài về tam giác - Định nghĩa, tính chất và cách chứng minh

Có một vài ba dạng tam giác đặc biệt quan trọng như sau:
II. Tam giác cân
1. Định nghĩa của tam giác cân
Tam giác cân nặng là tam giác sở hữu nhì cạnh mặt mũi vì thế cùng nhau.
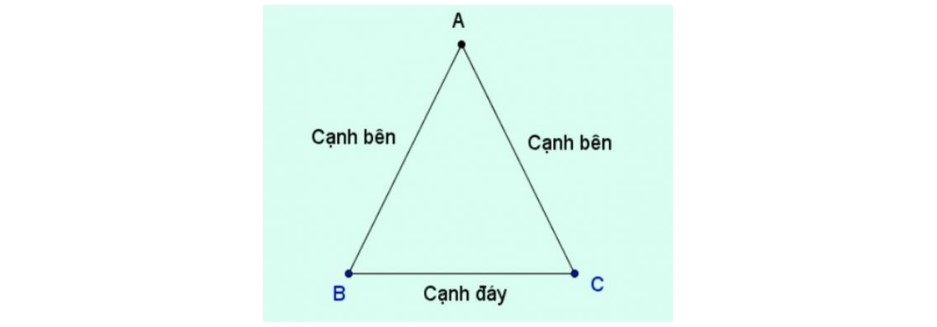
Từ hình vẽ bên trên, tao rất có thể xác lập được rằng:
– Đỉnh A của tam giác cân nặng ABC là phó điểm của cạnh mặt mũi AB và cạnh mặt mũi AC.
– Lúc này, góc BAC được gọi là góc ở đỉnh, nhì góc sót lại ABC và BCA là nhì góc lòng.
Cách dựng tam giác ABC cân nặng bên trên A
– Lấy điểm B và điểm C bất kì,nối nhau tạo nên cạnh BC
– Vẽ cung tròn trặn tâm B với nửa đường kính là r
– Vẽ cung tròn trặn tâm C với nửa đường kính là r
Hai cung tròn trặn phó nhau bên trên một điểm A và một điểm D.
Tam giác ABC hoặc tam giác DBC là tam giác cần thiết vẽ.
2. Tính hóa học về tam giác cân
– Tính hóa học 1: Trong tam giác cân nặng, nhì góc lòng vì thế cùng nhau.
Ví dụ: Tam giác OAB cân nặng bên trên đỉnh O ⇒ Góc A vì thế với góc B.
– Tính hóa học 2: Tam giác sở hữu nhì góc đều nhau là tam giác cân nặng.
Ví dụ: Tam giác BOD sở hữu góc O vì thế với góc D ⇒ Tam giác BOD cân nặng bên trên đỉnh B
– Tính hóa học 3: Trường phù hợp đặc biệt quan trọng của tam giác cân:
Tam giác vuông cân nặng là tam giác vuông sở hữu nhì cạnh của góc vuông vì thế cùng nhau.
Ví dụ: Tam giác MNP vuông bên trên M sở hữu góc N vì thế với góc P.. ⇒ Tam giác MNP vuông cân nặng bên trên đỉnh M.
Tính số đo từng góc nhọn của một tam giác vuông cân nặng.
Ta có: Δ ABC sở hữu góc A = 90°, góc B = góc C
⇒ góc B + góc C = 90° (định lí tổng tía góc vô và một tam giác)
⇒ 2.góc C = 90°
⇒ góc B = góc C = 45°
Kết luận: Tam giác vuông cân nặng thì nhì góc nhọn đều nhau và vì thế 45°.
III. Tam giác đều
1. Định nghĩa tam giác đều
Tam giác đều là tam giác sở hữu tía cạnh vì thế cùng nhau.
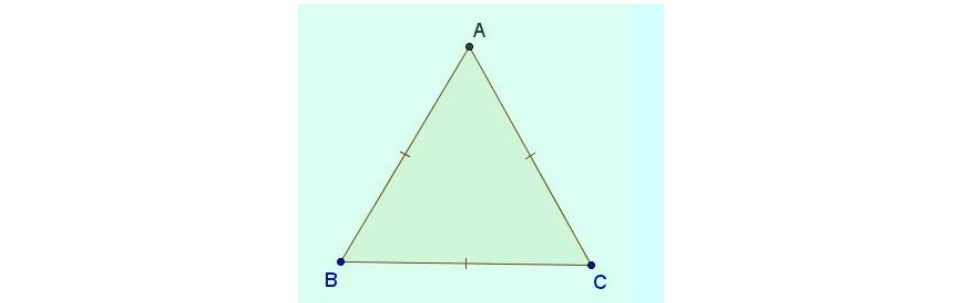
Cách dựng tam giác đều ABC
– Lấy điểm B và điểm C bất kì, nối lại tạo nên trở thành cạnh BC
– Vẽ (B; BC) và (C; BC)
– (B; BC) ∩ (C; BC) bên trên điểm A
ABC là tam giác đều cần thiết vẽ.
2. Tính hóa học của tam giác đều
– Tính hóa học 1: Trong tam giác đều từng góc đều đều nhau và vì thế 60 chừng.
Ví dụ: Tam giác OAB đều ⇒ Góc A = góc O = góc B = 60°
– Tính hóa học 2: Tam giác đều sở hữu tía lối cao vì thế cùng nhau.
– Tính hóa học 3: Tam giác đều sở hữu tía lối trung tuyến vì thế cùng nhau.
IV. Tam giác vuông
1. Định nghĩa Tam giác vuông
Tam giác vuông là tam giác sở hữu một góc vô tía góc vô tam giác là góc vuông (có số đo vì thế 90°).
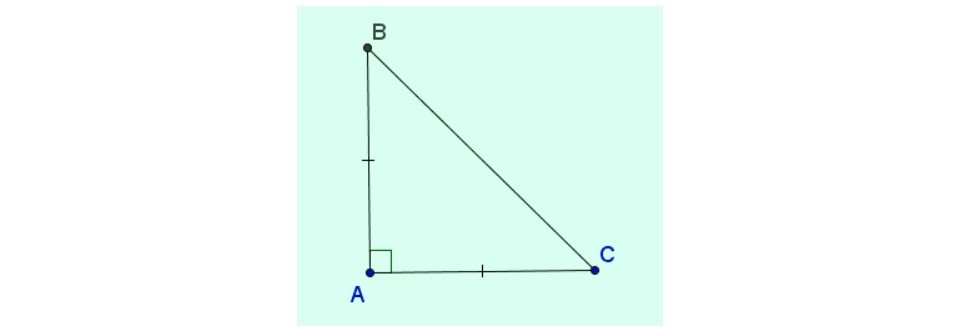
Cách dựng tam giác ABC vuông bên trên A
Cho trước cạnh huyền BC vì thế 4,5 centimet và cạnh góc vuông AC vì thế 2 centimet.
– Dựng đoạn AC vì thế 2 cm
– Dựng góc CAx vì thế 90 chừng.
– Dựng cung tròn trặn tâm C nửa đường kính là 4,5 centimet rời tia Ax bên trên điểm B. Nối điểm B và điểm C, tao được đoạn BC. Từ bại liệt tao sở hữu Δ ABC cần thiết dựng.
2. Tính hóa học của Tam giác vuông
– Tính hóa học 1: Trong tam giác vuông, nhì góc nhọn phụ nhau (nghĩa là tổng nhì góc vì thế 90 độ)
Ví dụ: Tam giác OAB vuông bên trên đỉnh O
⇒ Góc A + góc B = 90°
– Tính hóa học 2: Trong tam giác vuông, bình phương của cạnh huyền vì thế tổng bình phương của nhì cạnh góc vuông.
Ví dụ: Tam giác OAB vuông bên trên đỉnh O
⇒ OA² + OB² = AB²
– Tính hóa học 3: Trong tam giác vuông, lối trung tuyến ứng với cạnh huyền vì thế nửa số đo của cạnh huyền.
Ví dụ: Tam giác OAB vuông bên trên đỉnh O và sở hữu điểm M là trung điểm của đoạn AB
⇒ MO = MA = MB = nửa AB
1. Cách minh chứng tam giác là tam giác cân
– Cách 1: Chứng minh tam giác bại liệt sở hữu nhì cạnh vì thế cùng nhau.
– Cách 2: Chứng minh tam giác bại liệt sở hữu nhì góc vì thế cùng nhau.
Ví dụ: Trong tam giác ABC sở hữu tam giác ABD vì thế với tam giác ACD. Chứng minh tam giác ABC là tam giác cân nặng.
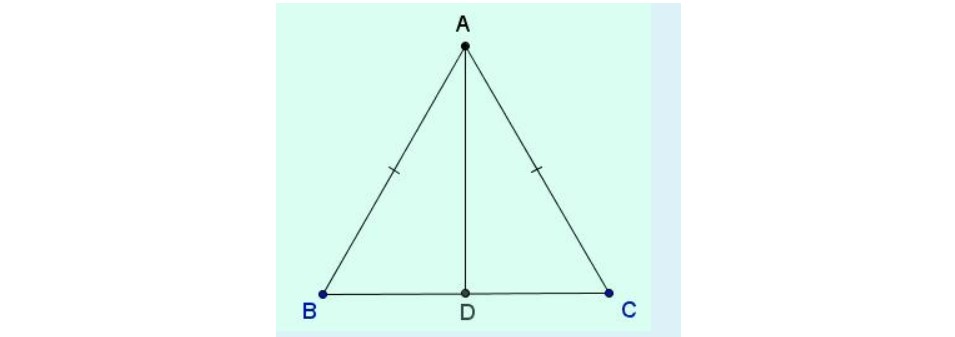
+ Chứng minh Theo phong cách 1:
Theo đề bài bác rời khỏi, tao có:
ΔABD = ΔACD
⇒ AB = AC
⇒ Tam giác ABC cân nặng bên trên đỉnh A
+ Chứng minh Theo phong cách 2:
Theo đề bài bác rời khỏi, tao có:
Xem thêm: 20 cách điều trị nám tàn nhang hiệu quả và nhanh chóng
ΔABD = ΔACD
⇒ Góc B = góc C
⇒ Tam giác ABC cân nặng bên trên đỉnh A
2. Cách minh chứng tam giác là tam giác đều
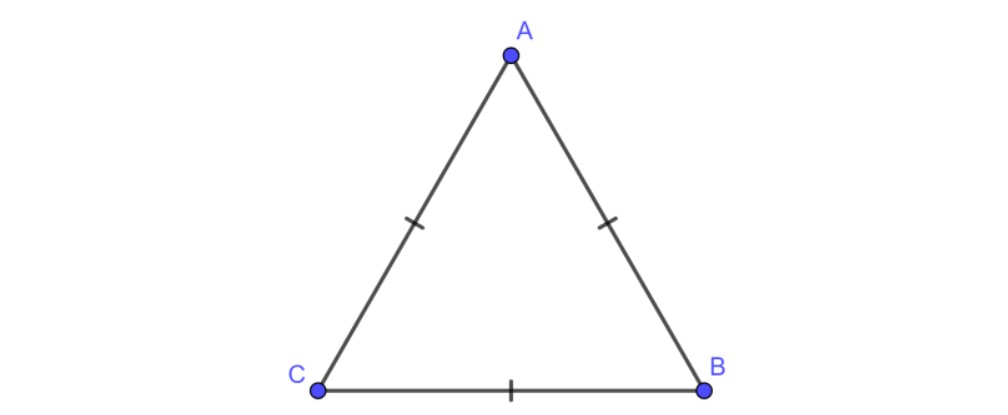
– Cách 1: Chứng minh tam giác bại liệt sở hữu tía cạnh vì thế cùng nhau.
Ví dụ: Tam giác CAB sở hữu CA = CB = AB
⇒ Tam giác CAB là tam giác đều
– Cách 2: Chứng minh tam giác bại liệt sở hữu 3 góc đều nhau.
Ví dụ: Chứng minh tam giác CAB sở hữu góc C = góc B = góc A
⇒ Tam giác CAB là tam giác đều
– Cách 3: Chứng minh tam giác bại liệt cân nặng và sở hữu một góc vì thế 60 chừng.
Ví dụ: Tam giác CAB sở hữu CA = CB và góc C = 60°
⇒ Tam giác CAB là tam giác đều
– Cách 4: Chứng minh tam giác bại liệt sở hữu 2 góc vì thế 60 chừng.
Ví dụ: Tam giác CAB sở hữu góc A = góc B = 60°
⇒ Tam giác CAB là tam giác đều
3. Cách minh chứng Tam giác vuông
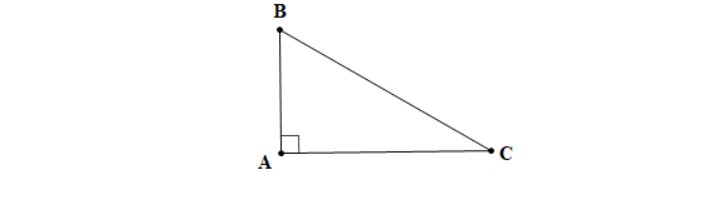
– Cách 1: Chứng minh tam giác bại liệt sở hữu 2 góc nhọn phụ cùng nhau.
Ví dụ: Tam giác CAB sở hữu góc C + góc B = 90°
⇒ Tam giác CAB vuông bên trên đỉnh A
– Cách 2: Chứng minh tam giác bại liệt sở hữu bình phương chừng lâu năm một cạnh vì thế tổng bình phương chừng lâu năm nhì cạnh sót lại.
Ví dụ: Tam giác Ngân Hàng Á Châu ACB sở hữu BA² + CA² = CB²
⇒ Tam giác CAB vuông bên trên đỉnh A
– Cách 3: Chứng minh tam giác bại liệt sở hữu lối trung tuyến ứng với cùng một cạnh vì thế nửa số đo của cạnh ấy.
Ví dụ: Tam giác CAB sở hữu M là trung điểm BC, biết MC = MA = MB = nửa BC
⇒Tam giác CAB vuông bên trên đỉnh A
– Cách 4: Chứng minh tam giác bại liệt nội tiếp một lối tròn trặn và sở hữu một cạnh là 2 lần bán kính của lối tròn trặn.
Ví dụ: Tam giác CAB nội tiếp lối tròn trặn 2 lần bán kính BC
⇒ Tam giác CAB vuông bên trên đỉnh A
C. BÀI TẬP CHỨNG MINH TAM GIÁC ĐẶC BIỆT
Bài 1: Trong những tam giác ở những hình a, b, c, d bên dưới, tam giác này là tam giác cân? Tam giác này là tam giác đều? Giải mến vì như thế sao?
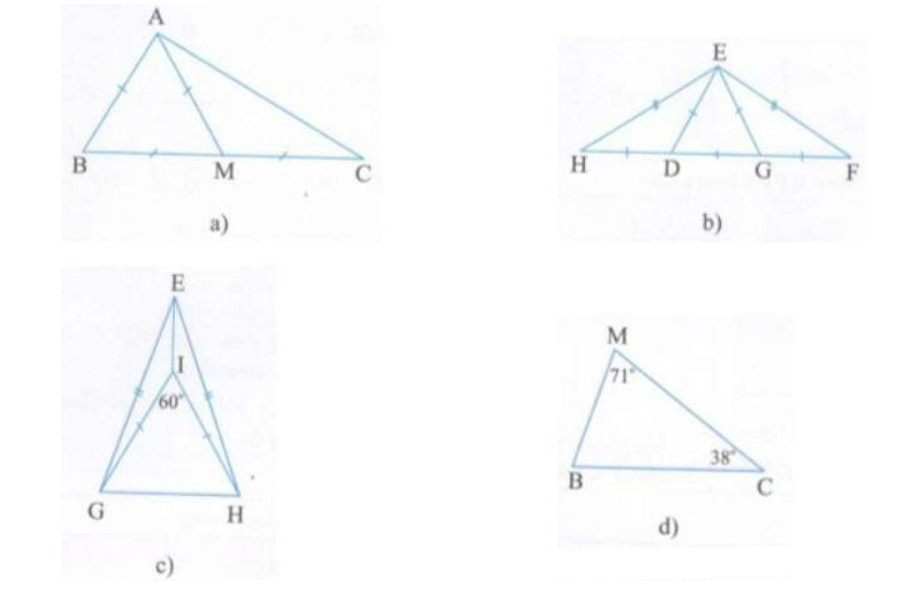
Hướng dẫn giải bài:
a) Ta có: AB = BM = AM (gt) ⇒ tam giác ABM là tam giác đều.
AM = CM (gt) ⇒ tam giác MAC cân nặng bên trên M.
b) Ta có: ED = DG = EG (gt) ⇒ tam giác EDG là tam giác đều.
DH = DE ⇒ tam giác DEH là tam giác cân nặng bên trên đỉnh D.
Ta có: EG = GF ⇒ tam giác GEF là tam giác cân nặng bên trên đỉnh G.
Ta có: EH = EF ⇒ tam giác EHF là tam giác cân nặng bên trên đỉnh E.
c) Ta có: IG = IH (gt) ⇒ tam giác IGH là tam giác cân nặng bên trên đỉnh I. Mà góc GIH=60 chừng (gt). Do bại liệt tam giác IGH là tam giác đều.
Ta có: EG = EH (gt) ⇒ tam giác EGH là tam giác cân nặng bên trên đỉnh E.
d) Tam giác MBC có: góc M + góc B + góc C = 180 độ
Do đó: 71 chừng + góc B + 38 chừng = 180 chừng ⇒ Góc B = 180 chừng – 71 chừng – 38 độ = 71 độ
Ta có: Góc B = góc M (cùng vì thế 71 độ) ⇒ ΔCBM cân nặng bên trên đỉnh C
Bài 2: Cho hình bên dưới, biết cạnh ED vì thế canh EF; nhận thêm EI là tia phân giác của góc DEF.
Chứng minh rằng:
a) ΔEID = ΔEIF.
b) ΔDIF cân nặng.
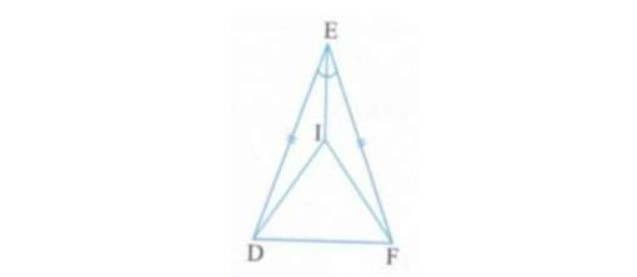
Hướng dẫn giải bài:
a) Xét tam giác EID và EIF tao có:
+ ED = EF (gt)
+ Góc IED= Góc EIF (EI là tia phân giác của góc DEF)
+ EI là cạnh công cộng.
⇒ Do đó: ΔEID =ΔEIF(c.g.c)
b) ΔEID =ΔEIF (chứng minh câu a) ⇒ cạnh ID vì thế cạnh IF. Do đó: tam giác DIF là tam giác cân nặng bên trên đỉnh I.
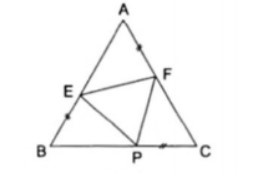
Bài 3: Cho Δ ABC là tam giác đều, bên trên cạnh AB lấy một điểm E, bên trên cạnh AC lấy một điểm F, bên trên cạnh BC lấy một điểm P.. sao mang đến chừng lâu năm tía cạnh BE, AF, PC đều nhau. Em hãy triệu chứng minh ΔEFP là tam giác đều.
Hướng dẫn giải bài:

Bài 4: Cho tam giác ABC sở hữu cạnh AB vì thế 6cm, cạnh AC vì thế 4,5cm, cạnh BC vì thế 7,5cm.
a) Chứng minh tam giác ABC là tam giác vuông bên trên đỉnh A. Tính số đo góc B, góc C và lối cao AH của tam giác bại liệt.
b) Hỏi rằng điểm M tuy nhiên diện tích S tam giác MBC vì thế diện tích S tam giác ABC phía trên đường thẳng liền mạch nào?
Hướng dẫn giải bài:
Xem thêm: Bạn đã biết – Cách tăng sức đề kháng cho người lớn

Trên đó là tổng phù hợp dạng bài bác về tam giác tuy nhiên HOCMAI vẫn tổ hợp dựa trên sách giáo khoa. Trong bài bác, sở hữu rất đầy đủ định nghĩa, đặc thù và cách thức minh chứng của những hình tam giác đặc biệt quan trọng. Các em làm rõ toàn bộ kỹ năng và kiến thức ở vô nội dung bài viết chưa nhỉ? HOCMAI vẫn tổ hợp tăng thiệt nhiều kỹ năng và kiến thức có ích nữa bên trên diaocalibaba.vn những em hãy xem thêm trang web này nhé!







![Top 10 Máy Massage Xung Điện tốt nhất 2024 [Tư Vấn Từ Bác Sĩ]](https://img.vn.my-best.com/contents/c9488d3dd73a0cc92ad682996bc6d56d.jpg?ixlib=rails-4.3.1&q=70&lossless=0&w=1200&h=900&fit=crop&s=468e1327fc6dd1d6c95aa2bf7b9d5162)




Bình luận