Xin xin chào toàn bộ chúng ta, hôm này tất cả chúng ta tiếp tục cùng với nhau mò mẫm hiểu về cách tính diện tích S của nhiều giác đều.
Mình tiếp tục trình diễn công thức tổng quát lác tuy nhiên song với công thức đặc trưng, ứng với từng nhiều giác (tam giác đều, tứ giác đều, ngũ giác đều, …)
Bạn đang xem: Cách tính diện tích đa giác đều (ngũ giác đều, lục giác đều…)
Việc thực hiện này sẽ hỗ trợ chúng ta có khá nhiều lựa lựa chọn rộng lớn khi cần thiết tính diện tích S nhiều giác, tương đương thể hiện tại được điểm mạnh và điểm yếu của từng công thức.
I. Đa giác đều là gì?
Một nhiều giác được gọi là nhiều giác đều nếu như nhiều giác thỏa mãn nhu cầu nhì ĐK được liệt kê bên dưới …
- Tất cả những cạnh cân nhau.
- Tất cả những góc cân nhau.
Tam giác đều, tứ giác đều (hình vuông), ngũ giác đều, lục giác đều, …, là những nhiều giác rất rất thông thường gặp gỡ vô Toán học tập tương đương vô thực tiễn.
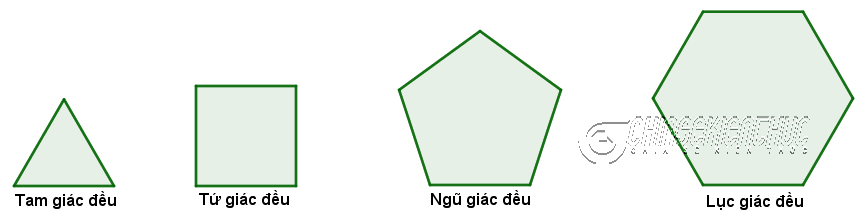
II. Một vài ba đặc điểm tiêu biểu vượt trội của nhiều giác đều
- Mỗi nhiều giác đều đều sở hữu một đàng tròn trĩnh nội tiếp và một đàng tròn trĩnh nước ngoài tiếp.
- Số đo từng góc của
ngiác đều được xem bám theo công thức $\frac{(n-2)180^o}{n}$
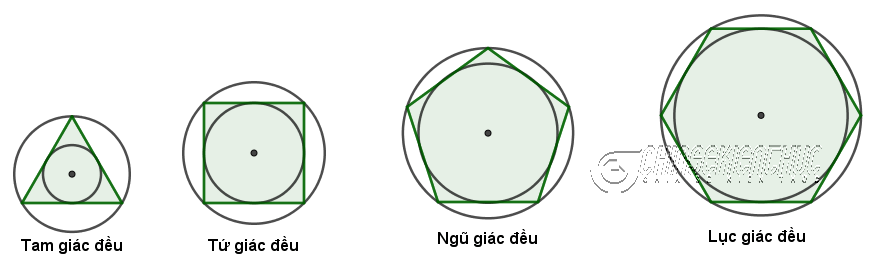
Ví dụ 1. Tính số đo từng góc của tam giác đều, tứ giác đều, ngũ giác đều và lục giác đều.
Vì tam giác đều sở hữu 3 cạnh nên số đo từng góc sẽ tiến hành tính bám theo công thức $\frac{(3-2)180^o}{3}=60^o$
Vì tam giác đều sở hữu 4 cạnh nên số đo từng góc sẽ tiến hành tính bám theo công thức $\frac{(4-2)180^o}{4}=90^o$
Vì tam giác đều sở hữu 5 cạnh nên số đo từng góc sẽ tiến hành tính bám theo công thức $\frac{(5-2)180^o}{5}=108^o$
Vì tam giác đều sở hữu 6 cạnh nên số đo từng góc sẽ tiến hành tính bám theo công thức $\frac{(6-2)180^o}{6}=120^o$
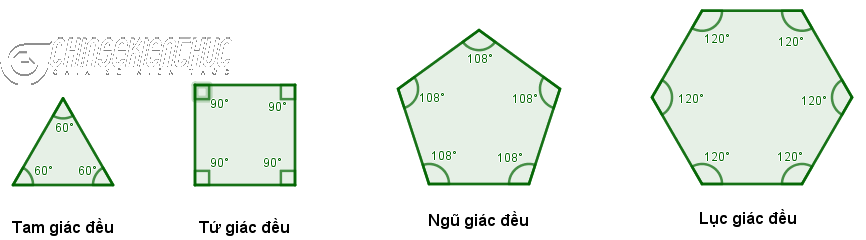
Chú ý: quý khách hàng nên ghi lưu giữ sự cân đối góc vô của nhiều giác đều, vì như thế lúc biết chừng nhiều năm một cạnh và sự cân đối một góc là bạn đã sở hữu thể vẽ được bọn chúng rồi.
- Góc ở tâm của n giác được xem bám theo công thức $\frac{360}{n}$
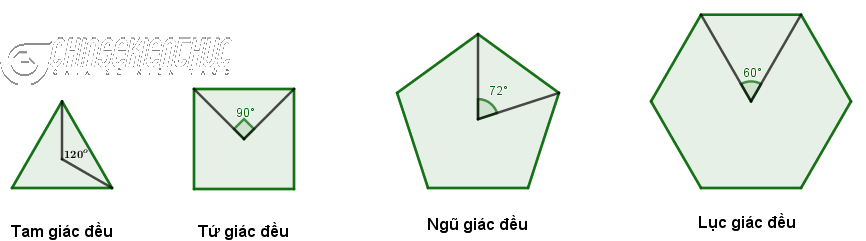
III. Trung đoạn là gì? Công thức tính chừng nhiều năm trung đoạn
Đoạn trực tiếp nối tâm của nhiều giác đều với trung điểm một cạnh được gọi là trung đoạn.
Độ nhiều năm trung đoạn của n giác với chừng nhiều năm cạnh a sẽ tiến hành tính bám theo công thức $\frac{a}{2} \cdot \cot \frac{\alpha}{2}$ (với $\alpha$ là góc ở tâm).
Ví dụ 2. Tính chừng nhiều năm trung đoạn của tam giác đều, tứ giác đều, ngũ giác đều và lục giác đều. thạo chừng nhiều năm từng cạnh của từng nhiều giác bên trên đều bên trên đều bằng a
- Vì tam giác đều sở hữu sự cân đối của góc ở tâm là $120^o$ nên chừng nhiều năm trung đoạn sẽ tiến hành tính bám theo công thức $\frac{a}{2} \cdot \cot \frac{120}{2}=\frac{\sqrt{3}}{3} \cdot \frac{a}{2}$
- Vì tứ giác đều sở hữu sự cân đối của góc ở tâm là $90^o$ nên chừng nhiều năm trung đoạn sẽ tiến hành tính bám theo công thức $\frac{a}{2} \cdot \cot \frac{90}{2}=\frac{a}{2}$
- Vì ngũ giác đều sở hữu sự cân đối của góc ở tâm là $72^o$ nên chừng nhiều năm trung đoạn sẽ tiến hành tính bám theo công thức $\frac{a}{2} \cdot \cot \frac{72}{2}=\cot 36 \cdot \frac{a}{2}$
- Vì lục giác đều sở hữu sự cân đối của góc ở tâm là $60^o$ nên chừng nhiều năm trung đoạn sẽ tiến hành tính bám theo công thức $\frac{a}{2} \cdot \cot \frac{60}{2}=\sqrt{3} \cdot \frac{a}{2}$
IV. Cách tính diện tích S nhiều giác đều
Tùy nằm trong vô fake thuyết của bài xích toàn thể hiện tuy nhiên tất cả chúng ta tiếp tục lưu ý đến và lựa lựa chọn công thức mang đến thích hợp nhất.
Trường hợp ý #1. thạo sự cân đối của góc ở tâm và chừng nhiều năm cạnh
Diện tích của n giác đều cạnh a và góc ở tâm $\alpha$ sẽ tiến hành tính bám theo công thức $S=\frac{n \cdot a^2}{4}\cdot \cot \frac{\alpha}{2}$
Ví dụ 3. Tính diện tích S tam giác đều ABC biết chừng nhiều năm cạnh $AB=2$
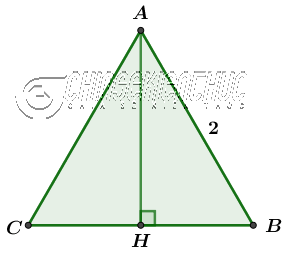
Lời giải:
Cách 1. sít dụng công thức $S=\frac{a^2 \cdot \sqrt{3}}{4}$
$S=\frac{2^2 \cdot \sqrt{3}}{4}=\sqrt{3}$
Cách 2. sít dụng công thức $S=\frac{1}{2}.CB.AH$
Chúng tớ vẫn biết chừng nhiều năm đàng cao vô tam giác đều cạnh $a$ bởi $\frac{a \cdot \sqrt{3}}{2}$
Suy đi ra $AH=\frac{2 \cdot \sqrt{3}}{2}=\sqrt{3}$
Vậy => $S=\frac{1}{2} \cdot 2 \cdot \sqrt{3}=\sqrt{3}$
Cách 3. sít dụng công thức $S=\frac{n \cdot a^2}{4} \cdot \cot \frac{\alpha}{2}$
Độ rộng lớn của góc ở tâm của nhiều giác đều được xem bám theo công thức $\alpha=\frac{360}{n}$
Suy đi ra $\alpha=\frac{360}{3}=120$
Vậy => $S=\frac{3 \cdot 2^2}{4} \cdot \cot \frac{120}{2}=\sqrt{3}$
Trường hợp ý #2. thạo chừng nhiều năm nửa đường kính đàng tròn trĩnh nước ngoài tiếp nhiều giác
Diện tích của n giác đều nội tiếp đàng tròn trĩnh tâm O nửa đường kính R sẽ tiến hành tính bám theo công thức $S=\frac{n}{2} \cdot R^2 \cdot \sin \frac{360}{n}$
Xem thêm: Vua Phụ Kiện - Cửa hàng Phụ kiện điện thoại, Sửa chữa điện thoại tại Hà Nội
Ví dụ 4. Tính diện tích S tứ giác đều ABCD biết chừng nhiều năm nửa đường kính đàng tròn trĩnh nước ngoài tiếp $R=3$
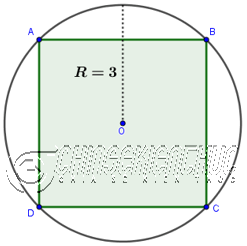
Lời giải:
Cách 1. sít dụng công thức $S=\frac{n}{2} \cdot R^2 \cdot \sin \frac{360}{n}$
Suy đi ra $S=\frac{4}{2} \cdot 3^2 \cdot \sin \frac{360}{4}=18$
Cách 2. sít dụng công thức $S=a^2$
Chúng tớ vẫn biết chừng nhiều năm cạnh của tứ giác đều nội tiếp đàng tròn trĩnh tâm O nửa đường kính R được xem bám theo công thức $\frac{2 \cdot R}{\sqrt{2}}$
Suy đi ra chừng nhiều năm cạnh của tứ giác đều vẫn nghĩ rằng $\frac{2 \cdot 3}{\sqrt{2}}=3\sqrt{2}$
Vậy => diện tích S của tứ giác đều vẫn mang đến bởi $(3\sqrt{2})^2=18$
Trường hợp ý #3. thạo chừng nhiều năm nửa đường kính đàng tròn trĩnh nội tiếp nhiều giác
Diện tích của n giác đều nước ngoài tiếp đàng tròn trĩnh tâm O nửa đường kính r sẽ tiến hành tính bám theo công thức $S=n \cdot r^2 \cdot \tan \frac{180}{n}$
Ví dụ 5. Tính diện tích S ngũ giác đều ABCDE biết chừng nhiều năm nửa đường kính đàng tròn trĩnh nội tiếp $r=5$
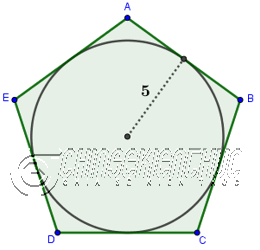
Lời giải:
Áp dụng công thức $S=n \cdot r^2 \cdot \tan \frac{180}{n}$
Suy đi ra $S=5 \cdot 5^2 \cdot \tan \frac{180}{5} \approx 90.8$
Vậy => diện tích S ngũ giác đều vẫn mang đến ngay gần bởi 90.8
Trường hợp ý #4. thạo chừng nhiều năm trung đoạn
Diện tích của n giác đều cạnh a trung đoạn d sẽ tiến hành tính bám theo công thức $S=\frac{1}{2} \cdot n \cdot a \cdot d$
Độ nhiều năm trung đoạn d sẽ tiến hành tính bám theo những công thức $d=\frac{a}{2} \cdot \cot \frac{\alpha}{2}=R \cdot \cos \frac{180}{n}=r$
V. Cách tính độ quý hiếm lượng giác Cot của một góc sử dụng máy tính CASIO
Máy tính CASIO fx-580VN X ko tương hỗ hàm $\cot$ nên tất cả chúng ta ko thể tính thẳng độ quý hiếm lượng giác $\cot$ của một góc được.
Vậy nên tất cả chúng ta tiếp tục tính loại gián tiếp trải qua hàm $\cos$ và $\sin$; hàm $\tan$
- Cách 1. $\frac{\cos(\square)}{\sin(\square)}$
- Cách 2. $\frac{1}{tan(\square)}$
- Cách 3. $\tan(\square)^{-1}$
Ví dụ 6. Tính độ quý hiếm lượng giác $\cot$ của góc $60^o$
Cách 1. $\frac{\cos(60)}{\sin(60)}$
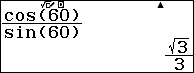
Cách 2. $\frac{1}{tan(60)}$

Cách 3. $\tan(60)^{-1}$

VI. Lời kết
Như vậy là những chúng ta cũng có thể thấy, công thức tổng quát lác nhất nhằm tính diện tích S của nhiều giác đều đó là công thức $\frac{1}{2} \cdot n \cdot a \cdot d$
Nếu fake thuyết mang đến chừng nhiều năm trung đoạn thì các bạn chỉ việc vận dụng công thức, còn nếu như không mang đến thì bạn phải mò mẫm chừng nhiều năm trung đoạn trước.
Ngoài đi ra bản thân sở hữu một vài khêu ý nhỏ ham muốn gửi cho tới những bạn:
- Nếu là nhiều giác đều đặc trưng thì nên vận dụng công thức đặc trưng.
- Bạn rất có thể minh chứng diện tích S tam giác đều cạnh và chừng nhiều năm một cạnh của hình vuông vắn bằng phương pháp phụ thuộc vào tấp tểnh lý Pytago.
Hi vọng là nội dung bài viết này tiếp tục hữu ích với các bạn. Xin Chào thân ái và hứa hẹn hội ngộ chúng ta trong mỗi nội dung bài viết tiếp theo sau !
Đọc thêm:
Xem thêm: Tuổi Canh Thìn sinh năm 2000 - Mệnh, Hợp tuổi và Màu sắc tương thích"
- Công thức tính DIỆN TÍCH TỨ GIÁC và CHU VI TỨ GIÁC
- Cách tính diện tích S và thể tích của hình trụ (có ví dụ)
- Cách tính Chu vi và Diện tích của hình thang (có ví dụ dễ dàng hiểu)
- Tính diện tích S, thể tích của hình lăng trụ đứng tam giác, tứ giác
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Bài viết lách đạt: 5/5 sao - (Có 1 lượt tiến công giá)
Note: Bài viết lách này hữu ích với các bạn chứ? Đừng quên review nội dung bài viết, lượt thích và share mang đến đồng minh và người thân trong gia đình của doanh nghiệp nhé !





.jpeg)




/https://admin.vuahanghieu.com/upload/news/2021/03/10-mau-dep-mlb-chinh-hang-nhat-dinh-phai-co-trong-tu-do-mua-he-17032021134903.jpg)
Bình luận